视频人体动作捕捉技术

视频人体动作捕捉技术

FesianXu 2020/08/25 at UESTC

前言

人体动作捕捉技术（简称人体动捕技术）是影视游戏行业中常用的技术，其可以实现精确的人体姿态，运动捕捉，但是用于此的设备昂贵，很难在日常生活中广泛应用。视频人体动作捕捉技术指的是输入视频片段，捕捉其中场景中的人体运动信息，基于这种技术，可以从互联网中海量的视频中提取其中的人体运动姿态数据，具有很广阔的应用场景。本文打算介绍视频人体动作捕捉相关的一些工作并且笔者的一些个人看法 。 如有谬误，请联系指出，转载请联系作者，并且注明出处。谢谢。

? 联系方式：

e-mail: FesianXu@gmail.com

QQ: 973926198

github: https://github.com/FesianXu

知乎专栏: 计算机视觉/计算机图形理论与应用

博客：

TensorFlow Using Chores?fesian.blog.csdn.net/

微信公众号：

人体动作捕捉技术

人体动作捕捉技术，简称人体动捕技术（Motion Capture, Mocap）是通过某些传感器，捕捉场景中人体运动的姿态或者运动数据，将这些运动姿态数据作为一种驱动数据去驱动虚拟形象模型或者进行行为分析。这里的传感器既可以是惯性传感器IMU，红外光信标（也可能是会发出红外光的摄像机），也可以是RGB摄像头或者是RGBD摄像头等。根据人体是否有佩戴传感器和佩戴的传感器是否会主动发送定位信号，我们可以把人体动捕技术大致分为：

1. 被动形式的人体动捕技术
2. 主动形式的人体动捕技术

被动形式的人体动捕技术

被动形式人体动捕：如Fig1.1和Fig1.2所示，此时人体佩戴的是会反射特定红外激光的光标，而在场景周围部署多个红外激光摄像头，这类型的激光摄像头会主动向人体发射特定的红外激光，该激光打到光标上会反射，摄像头通过接受这些反射光计算每个光标的空间位置。

Fig 1.1 人体佩戴着能够反射特定红外激光的光标，周围部署多个特定的红外激光摄像机。

Fig 1.2 基于红外光标的方案需要在场景周围部署多个特定的红外激光摄像头，成本高昂。

当然，现在基于RGB图片的人体姿态估计技术已经趋于成熟，目前已经有着很多很棒的相关工作[4,5]，我们以2D人体姿态估计为例子，通过部署多个经过相机标定的摄像头，我们在每个摄像头上都进行2D人体姿态估计得到每个人体的关节点，通过多视角几何，我们能够计算出关节点的空间位置。通过这种技术，人体不需要佩戴传感器或者光标，能够实现比较轻松的动作采集。这种技术我们称之为 视频人体动捕技术 ，其中采用了多个摄像头的我们称之为 多目视频人体动捕技术，如果只有单个摄像头，我们则称之为 单目视频人体动捕技术，而这也是本文的主要需要介绍的内容。

主动形式的人体动捕技术

主动形式的人体动捕技术需要人体佩戴特定传感器，这些传感器或可以自己发射特定的激光信息到周围部署的摄像头，实现多目定位，或可以通过牛顿力学原理计算初始位置记起的每个时刻的空间位置状态（我们称之为惯性导航），如Fig 1.3所示，该类型的方案通常比 被动形式的方案要精准，但是要求人体佩戴更为昂贵的专用设备，因此场景还是受限于大规模的影视游戏制作上。（虽然基于IMU的设备通常比红外激光设备要便宜，但是精度不如基于光学定位的，而且容易受到环境磁场的干扰）

Fig 1.3 人体佩戴主动式传感器，比如IMU，进行姿态相关的数据采集（比如旋转角，地磁，加速度等），然后计算出相对于初始位置的末态空间位置。

说回单目视频

单目RGB视频占据着目前互联网的大部分流量，是名副其实的流量之王。以人为中心的视频占据着这些视频的很大一部分，如果我们能较好的从其中提取出人体的动作和姿态信息，将能够很大程度上帮助我们进行更好的行为分析和虚拟动作生成，甚至可以在一定程度上取代之前谈到的依赖于专业设备的人体动捕技术，在影视游戏制作上助力。当然，基于单目视频毕竟存在某些信息的损失，比如自我遮挡，投影歧义性等，为了解决这些问题，或多或少要引入某些先验知识[21,22]。

单目视频人体动捕技术

从单目视频里面提取人体的动作信息，我们首先要知道什么称之为动作信息（motion）。在影视游戏领域，动作信息通常指的是 每个关节点相对于其父节点的旋转（rotation），以及整个骨架的朝向旋转（orientation）和偏移（translation） 。因为这个“动作信息”的定义贯穿着这整篇文章，因此笔者需要进行更为细致的介绍。

动作信息

在影视游戏领域，我们经常会要求动画师设计一个虚拟形象模型，如Fig 2.1所示。为了设计某些特定动作，我们通常会基于某个初始状态（一般是人体呈现T字形，称之为Tpose）进行修正得到最终需要的动作。为了实现这个修正，我们需要描述模型的每个关键部位，通常用关节点表示，如Fig 2.1所示，其中pelvis节点我们一般视为整个骨架的根节点，而其他的连接节点如果看成多叉树的话，就是子节点。这种树状结构，我们称之为 关节点树。

Fig 2.1 虚拟形象 初音未来 的Tpose模型，如果给虚拟模型绑定关节点，关节点的移动和旋转会带着蒙皮跟随变化。

除了根节点之外，其他所有节点都只有旋转信息（一般用欧拉角描述[6]），如Fig 2.2所示，通过三元组的欧拉角（即是分别围绕着XYZ轴旋转特定角度）旋转，可以实现大多数的空间旋转操作，从而修改模型的动作。注意到我们对于某个关节点进行旋转操作，那么其关节树下的其他子关节点也会跟着一起运动，这个和我们的常识是一致的。说回到根关节点，其旋转信息表示的是整个骨架的朝向，并且根节点还有偏移信息，可以表示骨架在世界坐标系下的空间位置。

Fig 2.2 欧拉角，分别绕着XYZ轴旋转特定角度，可以实现大多数空间旋转（有时候会存在万向节的现象）。

因此，通过一系列的旋转信息和偏移信息，我们可以描述一个骨架的一系列动作。

基本技术路线

从技术大方向来说，可以有以下两种思路：

1. 先从单目图片中提取出人体的关节点空间坐标数据，通常用欧式坐标表示。然后通过反向动力学（Inverse Kinematics，IK）计算得到每个关节点的旋转信息。
2. 直接通过模型从单目图片中估计出人体每个关节点的旋转信息。

一般来说，第一种方案是一种两阶段的方法，需要借助人体姿态估计的方法，比如[4,5]等去估计出2D人体姿态后，通过一些方法[7]可以从2D姿态数据中估计出3D姿态数据。当然也可以直接估计出3D姿态数据[8]，而不用2D姿态作为中间输入。然而单纯的欧式空间坐标还需要转换成旋转欧拉角才能满足后续的使用要求，为了实现这种转换，需要采用反向动力学的方式，去约束计算得到每个关节的旋转信息。这个转换的过程中存在着若干问题：

1. 反向动力学约束求解旋转信息计算速度慢，而且可能存在多解的情况，不是特别鲁棒。
   
2. 即便采用了反向动力学[9]去计算每个关节的旋转，但是某些关节（特别是双臂，双腿等可以自我旋转的）的“自旋转”是无法描述的，比如Fig 2.3所示，我们的中间输入是3D人体姿态，无法表述这种自旋转，因此即便采用了IK，计算得到的旋转角也会缺少一个自由度。当然，这个也并不是完全不能解决，如果姿态估计的结果能够精确到手指，给出部分手指的关节点数据，那么通过IK的约束还是可以恢复出手臂的自旋转的自由度的。
   

Fig 2.3 某些动作只存在肢体部分的自我旋转，也就是只有一个自由度的旋转，这种旋转即便采用IK也不能计算到，这部分的信息是完全的损失了。

鉴于这些问题，我们的第二种方案尝试直接从单目图片中估计人体的每个关节点的旋转信息，这种方案是一种一阶段的方案，只需要输入RGB图片，就可以输出每个关节点的旋转数据，而且这种方案有一定的机制可以恢复出双臂，双腿的自旋转自由度，因此该方案是本文的主要讨论内容，细节留到后文继续讲解。（注解：准确说，这里的“恢复出”不准确，应该是通过添加先验，把一些明显人体不能做出来的动作进行了排除）

基于运动估计的动捕技术

在本节中，我们主要讲解技术路线中第二种方案，也就是直接从RGB图片中估计人体每个关节点的旋转数据，我把这种方法称之为 基于运动估计的人体动捕 。 为了实现这个技术，必须要引入数字人体模型。数字人体模型是将人体形象参数化，使得可以通过若干个参数去表征人体的形状，动作等特征，数字人体模型有很多，比如SMPL模型[10] (该模型只能表示人体的基本属性，比如形状，运动，没有手势，表情等细节的参数化)，SMPL-X模型[11] (该模型是SMPL模型的扩展，可以表述手势，表情等细节)，Total Capture模型[12] （同样也是可以表征人体的基本属性，并且有手势，表情等细节）。

我们在之前的博客中介绍过最为流行的SMPL模型[10]，在本文稍微在介绍一下，更多细节请移步博文[10]，如有该基础的读者可以省略该部分内容。

SMPL模型

SMPL模型用以参数化人体模型的基本属性，比如动作姿态，形状等，该模型在[13]提出，其全称是Skinned Multi-Person Linear (SMPL) Model，其意思很简单，Skinned表示这个模型不仅仅是骨架点了，其是有蒙皮的，其蒙皮通过3D mesh表示，3D mesh如Fig 3.1所示，指的是在立体空间里面用三个点表示一个面，可以视为是对真实几何的采样，其中采样的点越多，3D mesh就越密，建模的精确度就越高（这里的由三个点组成的面称之为三角面片），具体描述见[14]。Multi-person表示的是这个模型是可以表示不同的人的，是通用的并且可以泛化到各个不同的人体的。Linear就很容易理解了，其表示人体的不同姿态或者不同升高，胖瘦（我们都称之为形状shape）是一个线性的过程，是可以控制和解释的（线性系统是可以解释和易于控制的）。那么我们继续探索SMPL模型是怎么定义的。

Fig 3.1 不同分辨率的兔子模型的3D mesh。

在SMPL模型中，我们的目标是对于人体的形状比如胖瘦高矮，和人体动作的姿态进行定义，为了定义一个人体的动作，我们需要对人体的每个可以活动的关节点进行参数化，当我们改变某个关节点的参数的时候，那么人体的姿态就会跟着改变，类似于BJD球关节娃娃[15]的姿态活动。为了定义人体的形状，SMPL同样定义了参数$\beta \in R^{10}$\beta \in \mathbb{R}^{10}，这个参数可以指定人体的形状指标，我们后面继续描述其细节。

Fig 3.2 SMPL模型定义的24个关节点及其位置。

总体来说，SMPL模型是一个数字人体参数化模型，其通过两种类型的参数对人体进行描述，如Fig 6所示，分别有：

1. 形状参数（shape parameters）：一组形状参数有着10个维度的数值去描述一个人的形状，每一个维度的值都可以解释为人体形状的某个指标，比如高矮，胖瘦等。
2. 姿态参数（pose parameters）：一组姿态参数有着$24\times 3$24 \times 3维度的数字，去描述某个时刻人体的动作姿态，其中的$24$24表示的是24个定义好的人体关节点，其中的$3$3并不是如同识别问题里面定义的$(x,y,z)$(x,y,z)空间位置坐标（location），而是指的是该节点针对于其父节点的旋转角度的轴角式表达(axis-angle representation)（对于这24个节点，作者定义了一组关节点树），当然，轴角式在计算中经常会换算成易于计算的欧拉角表达。

具体的$\beta$\beta和$\theta$\theta变化导致的人体mesh的变化的效果图可视化，大家可以参考博文[16]和[17]。

Fig 3.3 形状参数和姿态参数，原图出自[18]。

相信看到现在，诸位读者对于这种通过若干个参数去控制整个模型的姿态，形状的方法有所了解了，我们对于一个模型的形状姿态的mesh控制，一般有两种方法，一是通过手动去拉扯模型mesh的控制点以产生mesh的形变；二是通过Blend Shape，也就是混合成形的方法，通过不同参数的线性组合去“融合”成一个mesh。

基本技术路线

基于数字人体模型，我们只需要从RGB图片中估计出数字人体模型的参数即可，比如若使用SMPL数字人体模型，那么我们需要估计的参数有69+10+3+3=85个（这里的旋转使用了轴角式表达，因此只有3个参数，具体见[10]）：

1. 关节点的旋转信息，\theta \in \mathbb{R}^{23 \times 3}
2. 人体的形态参数，\beta \in \mathbb{R}^{10}
3. 相机外参数，\mathbf{t}_{\mathrm{cam}} \in \mathbb{R}^{2}， s \in \mathbb{R}^1， \mathbf{R} \in \mathbb{R}^{3}。

需要说明的是，我们一般假设渲染相机是弱透视相机[23,24]，意味着相机外参数有尺度缩放系数s和相对于场景的偏移\mathbf{t}_{\mathrm{cam}} = [\mathrm{tx},\mathrm{ty}]。需要注明的是，关节点中的根关节点，也就是Fig 3.2中的0号关节点的旋转信息是作为相机外参数看待的，表征了人体的朝向(orientation)信息，因此特别地，我们把该节点的旋转信息独立出，作为相机的旋转矩阵外参数，也就是有\mathbf{R} \in \mathbb{R}^{3}。

我们的基本思路就是通过模型去预测回归出SMPL模型参数。[19]中提到的HMR模型是一种经典的方法，如Fig 3.4所示，对于输入的场景，首先用检测算法对其中的人体位置进行确定并且裁剪得到人体的包围框。然后用Resnet-50 [25] 作为图片特征提取器，截取自最后的平均池化层的特征输出，得到图片特征\phi \in \mathbb{R}^{2048}。

为了更好地回归出SMPL模型参数，不能直接一次性地用网络回归出这些参数，而是通过迭代(iteration)的方式进行逐步的优化的。具体来说，如图Fig 3.5所示，首先初始化一个SMPL参数p \in \mathbb{R}^{85}，和特征输出\phi \in \mathbb{R}^{2048}进行拼接后，得到回归输入特征\Phi \in \mathbb{R}^{2133}。通过两层的全连接网络作为回归器，回归出SMPL模型参数p \in \mathbb{R}^{85}并将其反馈给输入前端，继续拼接并且循环刚才的过程。一般迭代次数设置T = 3。

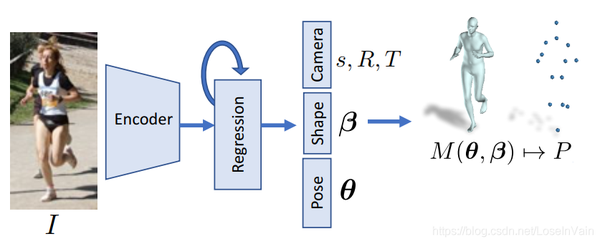
Fig 3.4 通过模型回归出人体的SMPL模型参数[19]。

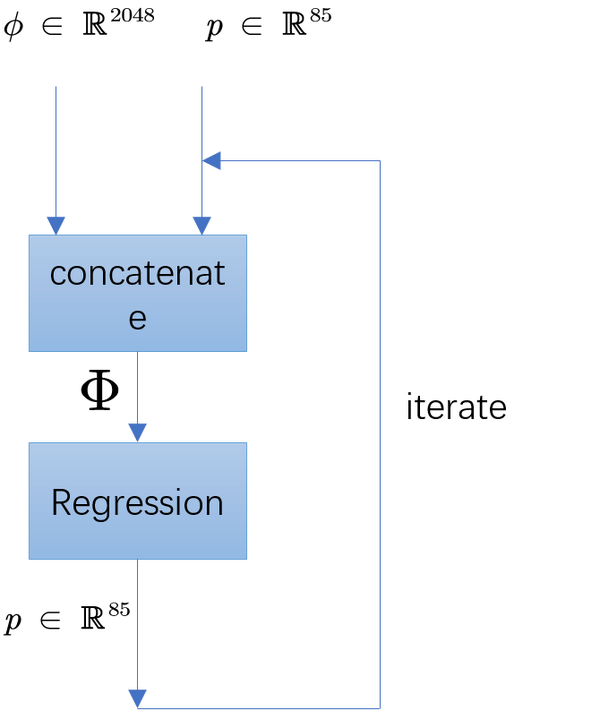
Fig 3.5 HMR中利用迭代去更好地回归出SMPL参数。

迭代过程的代码实例如下：

for i in range(n_iter):

    xc = torch.cat([x, pred_pose, pred_shape, pred_cam], 1)
    xc = self.fc1(xc)
    xc = self.drop1(xc)
    xc = self.fc2(xc)
    xc = self.drop2(xc)
    pred_pose = self.decpose(xc) + pred_pose
    pred_shape = self.decshape(xc) + pred_shape
    pred_cam = self.deccam(xc) + pred_cam

通过这个方法，我们可以回归出以上提到的SMPL参数，通过SMPL模型[26]可以生成数字虚拟人体模型，我们用M(\theta,\beta)表示该模型，通过弱透视相机（已经回归出外参数了），可以渲染得到二维平面投影，我们把这个过程表示为M(\theta,\beta) \stackrel{\mathbf{R}}{\rightarrow} P。

注意到这里的M(\theta,\beta) \in \mathbb{R}^{6890 \times 3}是人体模型的mesh，通过投影之后得到P \in \mathbb{R}^{6890 \times 2}。

为了实现后续谈到的训练，我们通常需要求得人体的控制点，也可以称之为关节点，具体求解过程见博文[10]。我们可以通过mesh求得其对于的关节点，如Fig 3.6所示，我们用X(\theta,\beta) \in \mathbb{R}^{24 \times 2}表示由 M(\theta,\beta) 解算得到的人体的24个关节点。

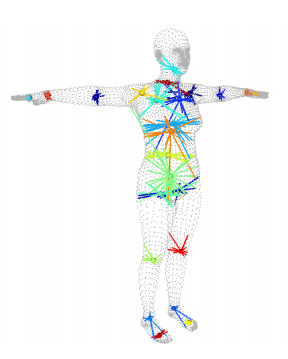
Fig 3.6 通过mesh求得人体的关节点。

为了实现训练，还需要进行3D关节点到2D关节点的投影，这个弱透视相机的投影过程可以表示为：

\hat{\mathbf{x}} = s\Pi(RX(\theta, \beta))+t \tag{3.1}

其中的\Pi(\cdot)是正交投影函数，见[27]。

训练阶段

我们在本节考虑如何去训练这个模型。我们的训练数据一般有两种类型的标注，一是2D的标注，2D标注可以由人工打标注而成，如Fig 3.7所示，这种数据的获取成本通常远比第二种方式的低很多；二是3D的标注，3D标注通常需要用专用设备，比如3D扫描仪进行扫描后标注，这种数据通常获取昂贵，不容易得到。

Fig 3.7 COCO数据中的2D关节点手工标注示例。

考虑到训练数据标注的多样性并且以2D标注为主，一般考虑用重投影(reprojection)得到的2D关节点作为预测进行损失计算。整个流程框图变成如Fig 3.8所示。

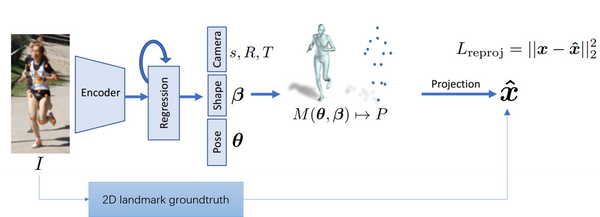
Fig 3.8 引入了重投影损失的框架。

用\mathbb{x}_i \in \mathbb{R}^{2}表示第i个真实标注的关节点的坐标，而v_{i} \in \{0,1\}^{24}表示这24个关节点在图中的可见性，被遮挡的部分设为0，可见部分设为1。那么，我们有重投影损失：

\mathcal{L}_{\mathrm{reproj}} = \sum_i ||v_i (\mathbf{x}_i-\hat{\mathbf{x}}_i)||_1 \tag{3.2}

考虑到某些数据集可能提供有3D标注，比如Human3.6m[28]。因此还可以引入可选的3D关节点监督损失，如：

\mathcal{L}_{\mathrm{3D \ joints}} = ||\mathbf{X}_i-\hat{\mathbf{X}}_i||^2_2 \tag{3.3}

其中\mathbf{X}_i \in \mathbb{R}^{24 \times 3}和\hat{\mathbf{X}}_i \in \mathbb{R}^{24 \times 3}分别是真实和预测的3D关节点。

同时，考虑到我们需要预测的是SMPL模型参数\hat{\theta},\hat{\beta}，因此有必要对该参数进行直接的监督，当3D MoCap数据可得的情况下，可以利用MoSh算法[29,30]求得对应的SMPL模型参数，记为[\beta, \theta]。于是我们有：

\mathcal{L}_{\mathrm{smpl}} = ||[\beta_i, \theta_i] - [\hat{\beta}_i, \hat{\theta}_i]||^2_2 \tag{3.4}

因此以整个3D关节点数据作为监督数据的损失为：

\mathcal{L}_{\mathrm{3D}} = \mathcal{L}_{\mathrm{3D \ joints}} + \mathcal{L}_{\mathrm{smpl}} \tag{3.5}

引入人体运动先验知识

我们在[10]中已经讨论过了2D到3D变换过程中固有的投影歧义性，如图Fig 3.9所示，简单来说就是

2D关节点到3D空间点的映射是具有歧义性的（ambiguous），因此对于同样一个2D关节点，在空间上就有可能有多种映射的可能性

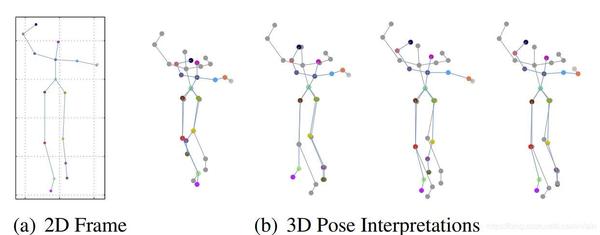
Fig 3.9 如果不对3D模型进行约束，那么单纯的单视角图像将会存在2D到3D投影的歧义性，如最后一张图的(a)是原始的2D节点，其到3D的投影有非常多的可能性。这里的歧义性可以由一定数量的多视角图像消除，或者通过对人体姿态的先验进行降低。

而如果想要在单目RGB图片中减少之中歧义性，就必须引入关于人体动作的先验，该先验描述了人体的极限动作范围，有些动作或者姿态，人体是不可能做到的（举个例子就是手臂自旋转180度，显然正常人类不可能做到），可以根据这个先验，排除掉一些模型预测出来的SMPL模型参数。同时，之前谈到过的某端肢体，比如双臂双腿的自旋转自由度的丢失问题，也可以通过该方式，进行一定的缓解。

为了引入这种先验知识，有多种方式，见[10]。常用的方法可以考虑通过建立大规模的真实人体3D数据集，这个数据集需要进行标准的参数化成数字人体模型，比如SMPL模型。然后通过对抗学习进行人体姿态正则的引入。因此在引入了对抗之后，整个网络的框图如Fig 3.10所示。

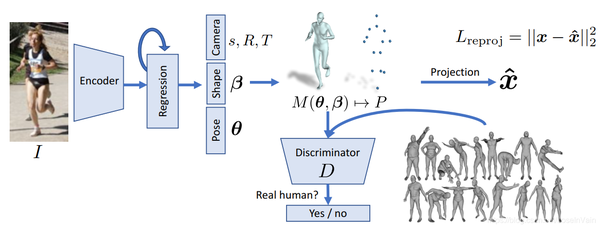
Fig 3.10 在HMR模型中，作者通过在大规模的真实人体mesh数据上进行对抗学习，从而引入了人体姿态正则。

注意到这里的判别器其实需要同时判断SMPL模型参数[\beta,\theta]是否是属于真实人体，为了更好地对每个关节点进行判别，需要对所有关节点分别设置一个判别器，并且考虑到全身的动作，同时也需要对全身的姿态进行判别，别忘了还需要对身体的形状参数\beta进行判别，因此一共有K+2个判别器，其中关节点数量K=24。每个判别器D_i输出的范围在[0,1]，表示了输入参数来自于真实数据的概率。

如果用E表示图片特征提取器，I表示图片输入，那么有对抗损失的数学表达形式：

\begin{aligned} \min_E \mathcal{L}_{adv}(E) &= \sum_i \mathbb{E}_{\Theta \sim P_E} [(D_i(E(I))-1)^2] \\ \min_{D_i} \mathcal{L}(D_i) &= \mathbb{E}_{\Theta \sim P_{\mathrm{data}}}[(D_i(\Theta)-1)^2]+\mathbb{E}_{\Theta \sim P_E} [D_i(E(I))^2] \end{aligned} \tag{3.6}

进而通过对抗损失，将人体运动先验引入了到了模型中。

考虑到时序信息

之前讨论的都是基于单帧的单目RGB图片进行处理的，而我们实际上需要考虑整段视频的处理。当然，简单地将视频分解为若干帧分别处理也能一定程度上解决问题，但是如果考虑到视频天然地一些特点：

1. 具有语义上的连续性
2. 具有动作语义

根据这些特点，我们可以引入更多的先验，从而规避由于单目RGB图片天然限制导致的一些歧义性。最典型的就是自遮挡导致的单帧估计误差，如Fig 3.11所示，我们注意到第三张图的左手被遮挡掉了，如果只考虑单帧估计，那么显然左手部分由于信息损失会出现歧义性，会出现很多奇怪的动作。然而如果考虑到视频上下文，我们可以对左手的大致位置进行估计，因而提高了鲁棒性。

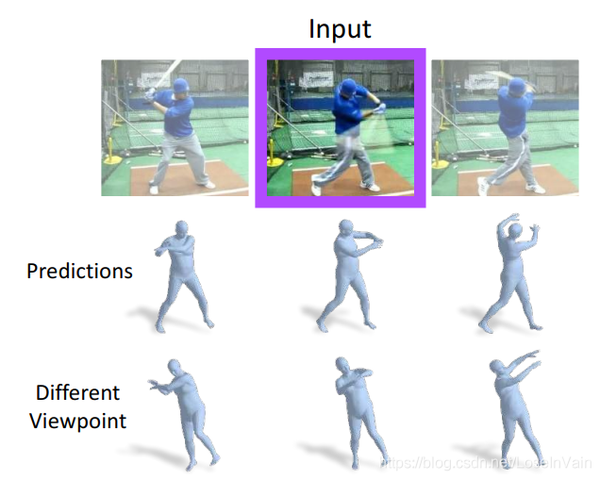
Fig 3.11 考虑到视频上下文的动作语义连续性，可以对某些帧的自遮挡部分进行修正。

考虑到视频的特点，从而引入时序上下文的工作有很多，比如[20, 31]。我们以[20]中提到的VIBE网络为例子，如Fig 3.12所示，其实我们发现和之前谈到的HMR模型差别不是特别大，只不过是在编码层引入了时序建模模块GRU网络[32]作为整个生成器（generator），其他的包括SMPL模型参数的估计和渲染相机的弱透视假设都是一致的。

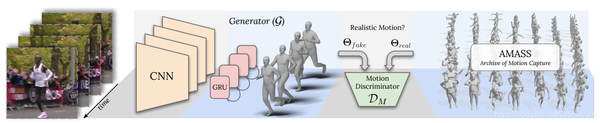
Fig 3.12 VIBE网络的网络框图。

假设输入帧为\mathbf{I} = \{I_1,\cdots,I_T\}，那么用f(\cdot)表示CNN图片特征提取网络，比如ResNet-50，有f_i \in \mathbb{R}^{2048}，用g(\cdot)表示GRU网络，那么我们有每帧的图片特征\mathbf{f} = \{f(I_1),\cdots,f(I_T)\}，经过了GRU网络后，我们有考虑到了时序上下文的特征，\mathbf{g} = \{g(f_1),\cdots,g(f_T)\}。考虑到人体的形状在视频中不应该出现明显的变化，因此我们对SMPL参数的损失函数，从式子(3.4)修改成式子(3.7)，意味着所有帧的人体形状都共用一个\beta。

\mathcal{L}_{\mathrm{smpl}} = ||\beta-\hat{\beta}||_2+\sum_{t=1}^T ||\theta_t - \hat{\theta}_t||_2 \tag{3.7}

当然，我们还需要修改判别器，使之可以考虑到时序上下文的语义信息，如Fig 3.13所示。这个扩展并不复杂，考虑到生成器输出的SMPL参数\hat{\Theta} = \{\beta, (\hat{\theta}_1,\cdots,\hat{\theta}_T)\}，为了对判别器的时序建模，我们在判别器中引入了GRU网络，用f_M表示。那么，每个隐层的输出为h_i = f_m(\hat{\Theta}_i)。为了将隐层输出序列[h_i,\cdots,h_T]聚合成一个单一的向量以便于判别，可以采用自注意力机制，学习出加权因子[\alpha_1,\cdots,\alpha_T]，有：

\begin{aligned} \phi_i &= \phi(h_i) \\ \alpha_i &= \dfrac{\exp(\phi_i)}{\sum_{t=1}^N \exp(\phi_t)} \\ r &= \sum_{i=1}^N \alpha_i h_i \end{aligned} \tag{3.8}

其中\phi(\cdot)是全连接网络。

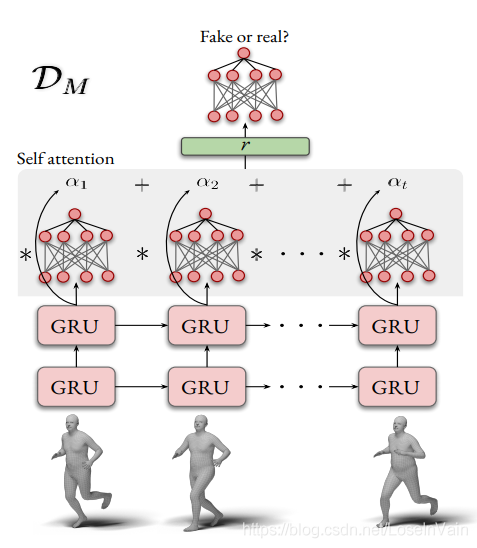
Fig 3.13 考虑到了时序上下文的判别器。

而整个对抗损失表示如下：

\begin{aligned} \mathcal{L}_{\mathrm{adv}} &= \mathbb{E}_{\Theta \sim p_G} [(\mathcal{D}_M(\hat{\Theta})-1)^2] \\ \mathcal{L}_{\mathcal{D}_M} &= \mathbb{E}_{\Theta \sim p_R} [(\mathcal{D}_M(\Theta)-1)^2]+\mathbb{E}_{\Theta \sim p_G} [\mathcal{D}_M(\hat{\Theta})^2] \end{aligned} \tag{3.9}

基于单目视频的优化

深度估计优化

单目RGB视频的限制意味着人体相对于相机的深度信息是不准确的，只能根据有限的场景信息去推断大致的深度信息。其中最为直接的是人体包围框的大小变化，我们知道在透视中，有着“远小近大”的现象。但是，如Fig 4.1所示，人体姿态会严重影响到人体包围框的大小尺度，因此如式子(4.1)所示，深度并不是人体包围框大小的线性函数。

d = g(\mathrm{scale}, \mathrm{pose},\cdots) \tag{4.1}

Fig 4.1 人体包围框大小会受到姿态的严重影响。

在专利 《基于视频的姿态数据捕捉方法和系统》(专利号：CN 109145788 A )中，作者提出了一种基于多线索去推理人体相对于相机的深度的方式。考虑到人体每个肢干的大小是不变的，我们可以把人体包围框的粒度缩小至人体肢干的包围框，或者更进一步，人体肢干的长度。有式子(4.2)

d = f \dfrac{\sqrt{\sum_i ||P^i_{[xy]}-\bar{P}_{[xy]}||^2}}{\sqrt{\sum_i ||K^i -\bar{K}||^2}} \tag{4.2}

其中f是焦距，可以简单设为参数，不影响整体比例；P^i_{[xy]} \in \mathbb{R}^2是2D姿态估计推理出来的平面关节点，而\bar{P}_{[xy]} \in \mathbb{R}^2是该帧所有2D姿态估计的平均值，其中v^i是可见性参数，判断是否关节点可见，因此v^i \in [0,1]^K，有：

\bar{P}_{[xy]} = \dfrac{1}{K}\sum^K_i v^i P^i_{[xy]} \tag{4.3}

而K^i \in \mathbb{R}^3是估计出来的3D关节点的空间坐标，\bar{K}是该帧所有3D关节点的空间坐标的平均值，有：

\bar{K} = \dfrac{1}{K} \sum_i^K v^i K^i \tag{4.4}

基于此的深度估计优化会比传统方案[31,20,19]的方法（即是只考虑人体包围框）更为鲁棒。

当然，鲁棒单目深度估计还有很多其他方法，篇幅所限按下不表。

高度估计优化

同样由于单目RGB输入的限制，我们的模型在预测渲染弱透视相机的外参数的时候，其中的偏移量\mathbf{t} = [t_x, t_y]是基于图像坐标参考系下而言的，而我们实际需要的坐标应该是基于世界坐标参考系而言的。这其中的差别使得我们预测出来的模型难以达到所谓的“绝对3D人体姿态估计（absolute 3D pose estimation）”的效果。这里谈到的“绝对（absolute）”意味着需要知道人体在世界坐标参考系下的坐标（至少要相对于地面来说是准确的，否则会出现人体模型浮空的现象）。

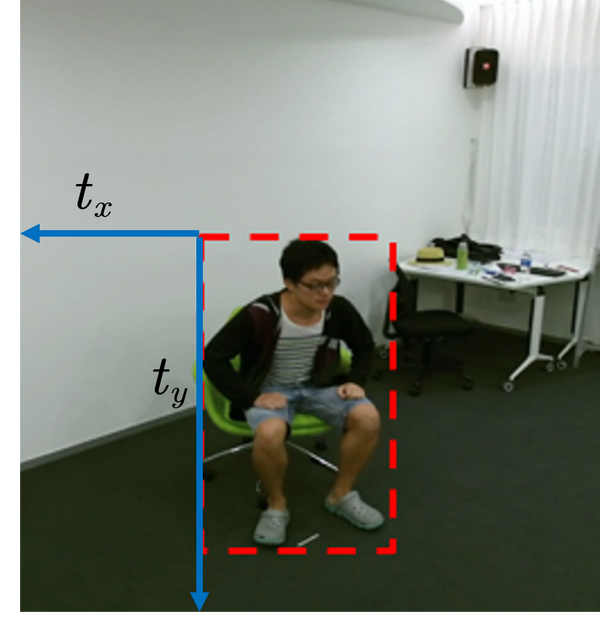
Fig 4.2 弱透视相机外参数的偏移是根据图像坐标参考系获取的，与世界坐标参考系存在一定的偏置，不解决这个问题是无法进行绝对人体3D姿态估计的。

已经有若干公开的工作讨论这里谈到的鲁棒高度估计，如[22,21]。其中在[22]中，作者考虑了通过检测地面与脚部的接触，同时通过物理优化去优化这部分的细节。

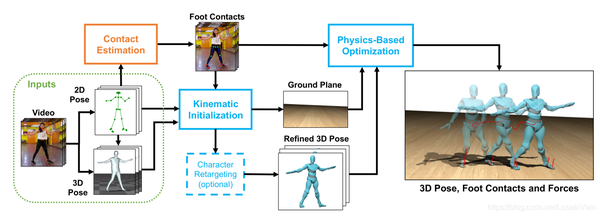
Fig 4.3 基于触地检测和物理优化的3D姿态估计，可以用于估计绝对3D人体姿态。

当然，鲁棒单目高度估计还有很多其他方法，篇幅所限按下不表。

Reference

[1]. Kocabas, Muhammed, Nikos Athanasiou, and Michael J. Black. "VIBE: Video inference for human body pose and shape estimation." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.

[2]. https://zhuanlan.zhihu.com/p/115049353

[3]. https://zhuanlan.zhihu.com/p/42012815

[4]. Cao, Z., Simon, T., Wei, S. E., & Sheikh, Y. (2017). Realtime multi-person 2d pose estimation using part affinity fields. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 7291-7299).

[5]. Fang, H. S., Xie, S., Tai, Y. W., & Lu, C. (2017). Rmpe: Regional multi-person pose estimation. In Proceedings of the IEEE International Conference on Computer Vision (pp. 2334-2343).

[6]. https://en.wikipedia.org/wiki/Euler_angles

[7]. Pavllo D, Feichtenhofer C, Grangier D, et al. 3D human pose estimation in video with temporal convolutions and semi-supervised training[J]. arXiv preprint arXiv:1811.11742, 2018.

[8]. Pavlakos, G., Zhou, X., Derpanis, K. G., & Daniilidis, K. (2017). Coarse-to-fine volumetric prediction for single-image 3D human pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 7025-7034).

[9]. https://en.wikipedia.org/wiki/Inverse_kinematics

[10]. https://blog.csdn.net/LoseInVain/article/details/107265821

[11]. Pavlakos, G., Choutas, V., Ghorbani, N., Bolkart, T., Osman, A. A., Tzionas, D., & Black, M. J. (2019). Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 10975-10985).

[12]. Joo, H., Simon, T., & Sheikh, Y. (2018). Total capture: A 3d deformation model for tracking faces, hands, and bodies. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 8320-8329).

[13]. Loper M, Mahmood N, Romero J, et al. SMPL: A skinned multi-person linear model[J]. ACM transactions on graphics (TOG), 2015, 34(6): 1-16.

[14]. https://whatis.techtarget.com/definition/3D-mesh

[15]. https://baike.baidu.com/item/BJD%E5%A8%83%E5%A8%83/760152?fr=aladdin

[16]. https://www.cnblogs.com/xiaoniu-666/p/12207301.html

[17]. https://blog.csdn.net/chenguowen21/article/details/82793994

[18]. https://khanhha.github.io/posts/SMPL-model-introduction/

[19]. Kanazawa, A., Black, M. J., Jacobs, D. W., & Malik, J. (2018). End-to-end recovery of human shape and pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 7122-7131).

[20]. Kocabas, M., Athanasiou, N., & Black, M. J. (2020). VIBE: Video inference for human body pose and shape estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 5253-5263).

[21]. Zhen, J., Fang, Q., Sun, J., Liu, W., Jiang, W., Bao, H., & Zhou, X. SMAP: Single-Shot Multi-Person Absolute 3D Pose Estimation. ECCV 2020

[22]. Rempe, Davis, Leonidas J. Guibas, Aaron Hertzmann, Bryan Russell, Ruben Villegas, and Jimei Yang. "Contact and Human Dynamics from Monocular Video." Proceedings of the European Conference on Computer Vision (ECCV) 2020

[23]. https://blog.csdn.net/LoseInVain/article/details/102883243

[24]. https://blog.csdn.net/LoseInVain/article/details/102698703

[25]. He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Identity mappings in deep residual networks." In European conference on computer vision, pp. 630-645. Springer, Cham, 2016.

[26]. https://github.com/CalciferZh/SMPL

[27]. https://blog.csdn.net/LoseInVain/article/details/102698703

[28]. http://vision.imar.ro/human3.6m/description.php

[29]. M. Loper, N. Mahmood, and M. J. Black. MoSh: Motion and shape capture from sparse markers. ACM Transactions on Graphics (TOG) - Proceedings of ACM SIGGRAPH Asia, 33(6):220:1–220:13, 2014

[30]. G. Varol, J. Romero, X. Martin, N. Mahmood, M. J. Black, I. Laptev, and C. Schmid. Learning from Synthetic Humans. In CVPR, 2017

[31]. Kanazawa, A., Zhang, J. Y., Felsen, P., & Malik, J. (2019). Learning 3d human dynamics from video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 5614-5623).

[32]. Cho, K., Van Merri?nboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.